Algorytm k-średnich – uczenie nienadzorowane
 Algorytm k-średnich (z ang. k-means) inaczej zwany również algorytmem centroidów, służy do podziału danych wejściowych na z góry założoną liczbę klas. Jest to jeden z algorytmów stosowany w klasteryzacji (grupowaniu) i jest częścią uczenia nienadzorowanego w Machine Learning.
Algorytm k-średnich (z ang. k-means) inaczej zwany również algorytmem centroidów, służy do podziału danych wejściowych na z góry założoną liczbę klas. Jest to jeden z algorytmów stosowany w klasteryzacji (grupowaniu) i jest częścią uczenia nienadzorowanego w Machine Learning.
Aby dobrze zrozumieć zasady działania tego algorytmu musimy wprowadzić jedno nowe pojęcie: „centroid„. Centroid jest to reprezentant danego skupienia lub inaczej środek danej grupy.
Podstawowa zasada działania
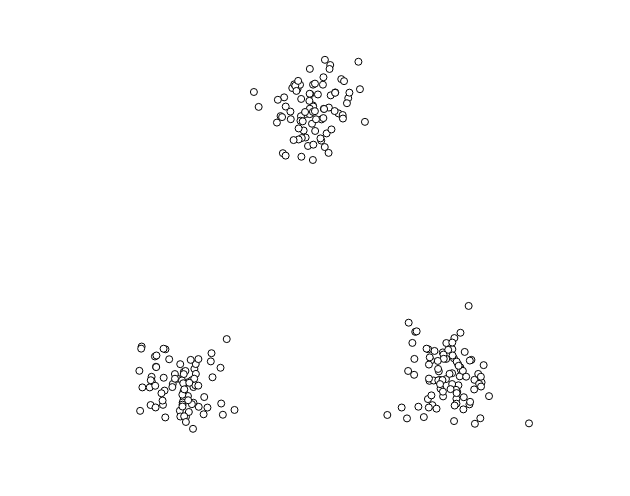
Dla dobrej wizualizacji działania algorytmu k-średnich proponuję zbiór punktów ułożonych na płaszczyźnie w 3 różnych skupiskach. Na początku zakładamy, że przynależność poszczególnych punktów do klas (etykiet) nie jest nam znana.
Krok pierwszy
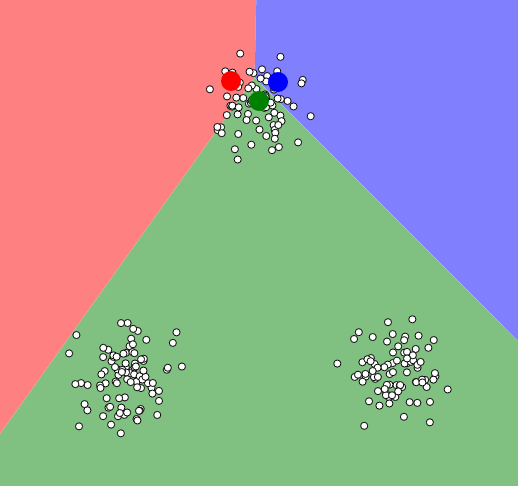
Wybór ilości centroidów i początkowe ułożenie ich w przestrzeni. Tak jak napisałem na wstępie, dla tego algorytmu musimy z góry określić na ile grup chcemy podzielić nasz zbiór. Następnie umieszczamy w przestrzeni zadaną ilość punktów. Sposób rozmieszczenia ma ogromne znaczenie i zależy od niego ostateczny wynik działania algorytmu. Stosuje się tutaj różne techniki, aby zoptymalizować jego pracę. Ja umieszczę trzy punkty w losowych miejscach:
Krok drugi
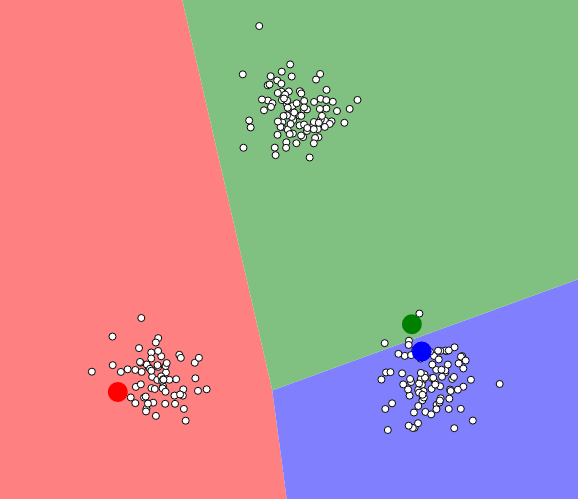
Teraz ustalamy przynależność punktów do naniesionych centroidów. Jak widać na poprzednim obrazie wszystkie punkty były białe. W tym kroku wyliczamy średnie odległości poszczególnych punktów i przypisujemy najbliższym im centroid (w naszym przypadku będzie to przypisanie koloru):
Krok trzeci
Aktualizujemy położenie naszych centroidów. Nowe współrzędne centroidów to średnia arytmetyczna współrzędnych wszystkich punktów mających jego grupę (są też inne techniki). Zobaczmy jak przemieszczą się punkty w naszym przykładzie (zauważcie, że przynależność samych punktów nie zmieniła się, na tym etapie przesuwamy same środki):
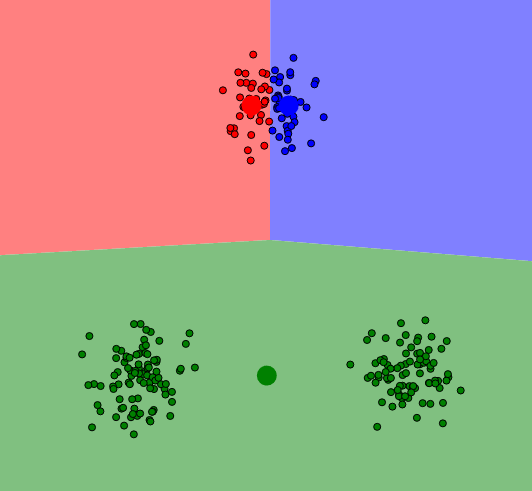
Zakończenie algorytmu
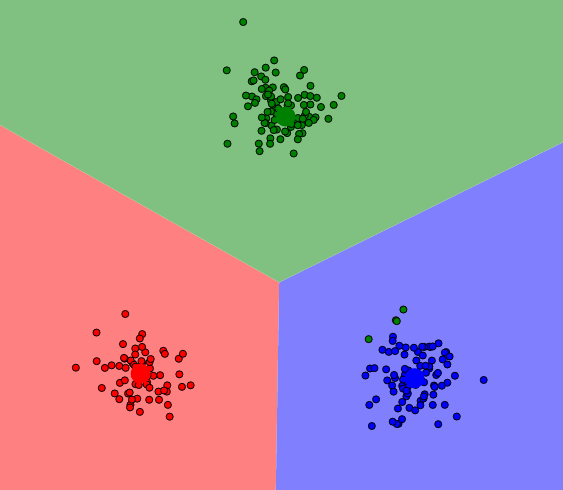
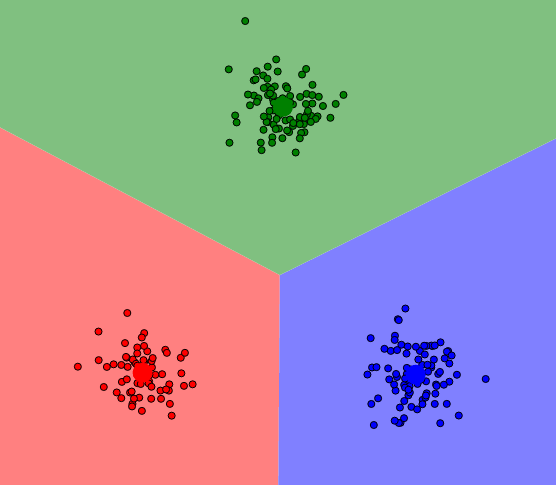
Krok drugi i trzeci powtarzamy aż do osiągnięcia kryterium zbieżności, którym najczęściej jest stan w którym nie zmieniła się przynależność punktów do klas. Dla naszego przykładu osiągniemy ostateczny krok już po drugiej iteracji:
Problem z inicjalizacją centroidów
W powyższym przykładzie zbiór danych został pogrupowany zgodnie z naszą „intuicją” na trzy grupy, ale wszystko zależy od początkowego ułożenia punktów startowych centroidów. Zobaczcie do czego może doprowadzić takie początkowe ułożenie:
W skutek 3 iteracji otrzymamy następujący wynik:
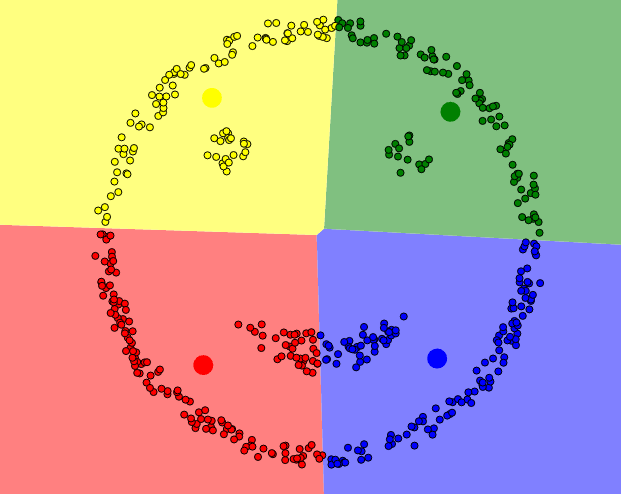
Jedną ze strategii obrony jest wybór punktów początkowych, które będą od siebie „maksymalnie” oddalone. Niestety nie zawsze daje to dobre rezultaty. Poniższy przykład pokazuje, że pogrupowane dane nie zawsze odzwierciedlają naszą intuicję. Być może chcielibyśmy podzielić ten zbiór w trochę inny sposób:
Podsumowanie
Algorytm k-średnich:
- wstępnie ustalamy parametr k czyli liczbę grup na które chcemy podzielić nasze dane wejściowe
- działamy do momentu stabilizacji czyli gdy nie dochodzi już do żadnych zmian w uzyskanych grupach.
- wykorzystujemy miarę odległości między punktami (zwykle euklidesową)
Możliwe ulepszenia lub modyfikacje:
- różne sposoby znajdowania odległości
- zmiana liczby grup w trakcie pracy algorytmu (zapobieganie nadmiernej unifikacji i przesadnemu rozdrobnieniu)
- wykorzystanie warzonej miary odległości uwzględniającej znaczenie atrybutów
Zalety algorytmu k-średnich:
- niska złożoność, a co za tym idzie wysoka wydajność działania
- przy dużych zbiorach i niskich ilościach grupa algorytm ten będzie zdecydowanie szybszy niż pozostałe algorytmy tej klasy
- pogrupowane zbiory są z reguły bardziej ciaśniejsze i zbite
Wady:
- nie pomaga w określeniu ilości grup (K)
- różne wartości początkowe prowadzą do różnych wyników
- działa dobrze tylko dla „sferycznych” skupisk o jednorodnej gęstości
Do wizualizacji wszystkich przykładów wykorzystałem narzędzie autorstwa Naftali Harris (@naftaliharris) dostępny na stronie: http://www.naftaliharris.com/blog/visualizing-k-means-clustering/
Entuzjasta programowania. Z zawodu web developer. Pragmatyk. Od jakiegoś czasu również przedsiębiorca. Racjonalista. W wolnych chwilach biega i bloguje. Miłośnik gier i grywalizacji. Więcej na jego temat znajdziesz w zakładce „O mnie” tego bloga.